Estratégia de trading de Fibonacci
Escrito por Aaron Akwu, Chefe de Educação Hantec Markets
Introdução
Este um método de análise e realização de negociações com base na sequência de Fibonacci, que é uma série de números em que cada um é a soma dos dois anteriores 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, etc.). As retrações de Fibonacci são usadas pelos traders em finanças para determinar níveis prováveis de suporte e resistência no movimento de preços de um ativo. O cálculo desses níveis é feito determinando as distâncias verticais entre os pontos altos e baixos do preço de um ativo e, em seguida, dividindo essas distâncias pelas principais razões de Fibonacci (23,6%, 38,2%, 50%, 61,8%, e 100%). Se um preço voltar a um desses níveis após um movimento significativo para cima ou para baixo, isso pode indicar uma possível mudança na tendência, e essas informações podem ser usadas para tomar decisões de compra ou venda.
Origens do Fibonacci ou da "Proporção Áurea"
Os números de Fibonacci e a proporção áurea remontam ao antigo matemático Leonardo de Pisa, também conhecido como Fibonacci. Em 1202, ele publicou seu livro “Liber Abaci”, em que introduziu a sequência de números agora conhecida como sequência de Fibonacci. A sequência começa com 0 e 1, e cada número subsequente é a soma dos dois números anteriores. Ela aparece em muitos fenômenos naturais, como os padrões de crescimento de plantas e animais.
A proporção áurea é um conceito matemático que descreve a relação entre duas quantidades em que a razão da menor para a maior é a mesma que a razão da maior para a soma de ambas. Ela é aproximadamente igual a 1,6180339887 e representada pela letra grega phi (φ). Está presente em diversas estruturas naturais e artificiais e é considerada um princípio universal de beleza e harmonia.

Por que o Fibonacci é relevante para os mercados financeiros?
A sequência de Fibonacci é importante para os mercados financeiros porque é usada para identificar potenciais níveis de suporte e resistência para o preço de um ativo financeiro. Ela é derivada da adição dos dois números anteriores para obter o próximo número, começando de 0 e 1. Na análise técnica, traders e investidores usam retrações de Fibonacci para identificar níveis nos quais o preço de um ativo pode encontrar suporte ou resistência após um movimento de preço. Esses níveis são determinados calculando a retração percentual do movimento do preço e encontrando o nível correspondente na sequência de Fibonacci. Os mais usados são 23,6%, 38,2%, 50%, 61,8% e 100%. Eles são considerados significativos porque correspondem frequentemente a níveis psicológicos importantes em trading e podem representar áreas para os traders entrarem ou saírem de posições.
Retração e extensão de Fibonacci
Essa é uma ferramenta de análise técnica que utiliza linhas horizontais para identificar níveis de suporte e resistência no movimento de preços de um ativo. Os traders podem traçar as oscilações de preço de alta para baixa e usar a proporção de Fibonacci de 23,6%, 38,2%, 50%, 61,8% e 100% para prever onde o preço pode retroceder ou se estender. Os níveis de retração de Fibonacci são usados para determinar os níveis de suporte, enquanto os níveis de extensão são usados para identificar onde é possível lucrar. Eles são utilizados com frequência no trading de Forex, ações e criptomoedas como fonte de informações que ajudam a aumentar as chances de sucesso.
O que é a retração de Fibonacci?
Trata-se de uma ferramenta de análise técnica que usa linhas horizontais para indicar áreas de suporte ou resistência nos principais níveis de Fibonacci antes que o preço continue na direção original. Os níveis de retração de Fibonacci mais utilizados são 38,2%, 50% e 61,8%. Os traders técnicos que usam essa ferramenta conseguem ter uma boa vantagem no mercado. Ela é um dos recursos de trading mais comuns no software de gráficos (MT4/MT5).
Digamos que um ativo esteja sendo negociado em $100, mas o preço sobe para $150 durante um período. Para traçar os níveis de retração, você primeiro encontra a diferença entre o preço alto e baixo: $150 – $100 = $50. Depois, multiplica essa diferença pelas principais razões de Fibonacci (0,382, 0,5 e 0,618) e adiciona o resultado ao preço baixo.
Nível de retração de 38,2%: $100 + ($50 x 0,382) = $119.10
Nível de retração de 50%: $100 + ($50 x 0,5) = $125
Nível de retração de 61,8%: $100 + ($50 x 0,618) = $130.90
Esses níveis seriam então traçados em um gráfico de forma horizontal e usados como áreas potenciais de suporte ou resistência. Os traders podem considerar a possibilidade de assumir uma posição de compra ou venda se o preço do ativo se recuperar e atingir um destes níveis, dependendo da direção do movimento dos preços.
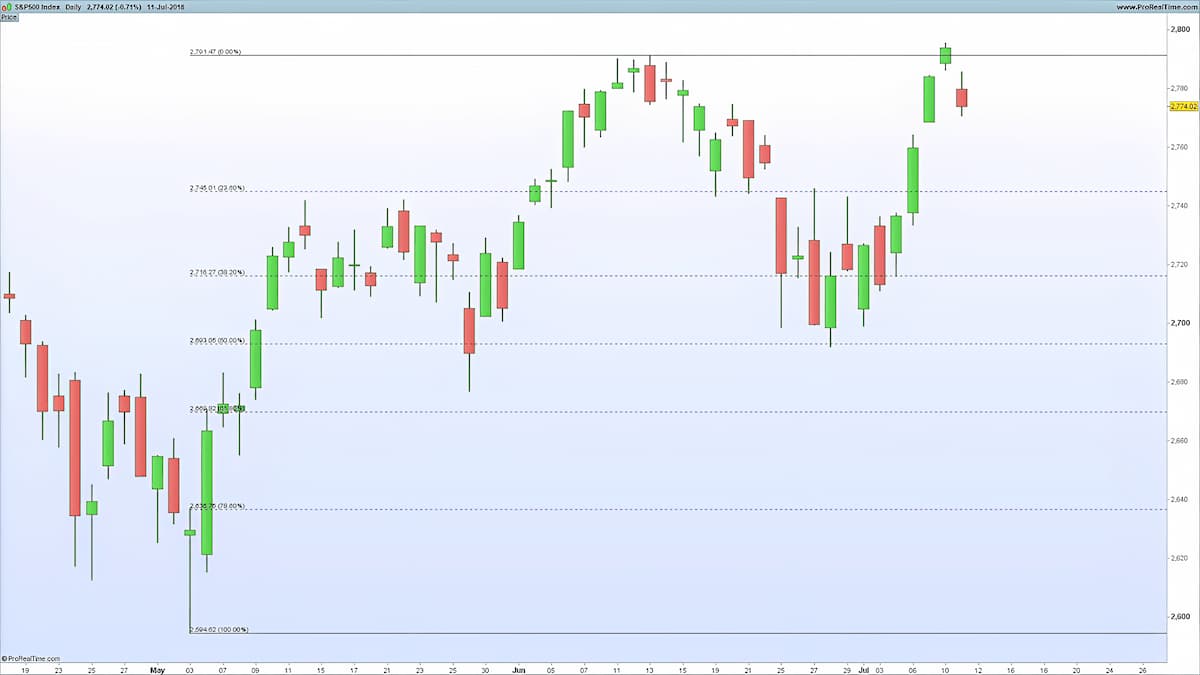
O que é a extensão de Fibonacci?
Essa é uma ferramenta de análise técnica usada para identificar níveis de suporte e resistência nos mercados financeiros. Ela se baseia na sequência de Fibonacci, uma série de números em que cada um é a soma dos dois anteriores (0, 1, 1, 2, 3, 5, 8, 13, 21, etc.). Na análise técnica, os níveis de Fibonacci mais utilizados são 0,0%, 23,6%, 38,2%, 50,0%, 61,8%, e 100,0%.
Veja como ela pode ser usada no trading de moedas:
Digamos que você queira negociar ações XYZ. Depois de analisar os gráficos, você determina que a ação recentemente teve um movimento significativo de $100 para $150. Você pode usar extensões de Fibonacci para saber onde a ação encontrará suporte ou resistência em seu próximo movimento.
Trace a extensão de Fibonacci da oscilação baixa para a alta, que neste caso é de $100 a $150.
O nível de extensão de 38,2% é calculado multiplicando a diferença entre a oscilação alta e a oscilação baixa por 0,382 e, em seguida, adicionando o resultado à oscilação baixa. Nesse caso, esse nível é de $119.10.
O nível de extensão de 50,0% é calculado multiplicando a diferença entre a oscilação alta e a oscilação baixa por 0,5 e, em seguida, adicionando o resultado à oscilação baixa. Nesse caso, esse nível é de $125.
O nível de extensão de 61,8% é calculado multiplicando a diferença entre a oscilação alta e a oscilação baixa por 0,618 e, em seguida, adicionando o resultado à oscilação baixa. Nesse caso, esse nível é de $130.90.
Se a ação se aproximar de um desses níveis, os traders podem encarar isso como uma oportunidade para entrar em uma negociação, pois ela pode encontrar suporte no nível e se recuperar. Se a ação ultrapassar esses níveis, os traders podem considerar sair de suas posições, pois isso pode indicar que a ação está perdendo força.
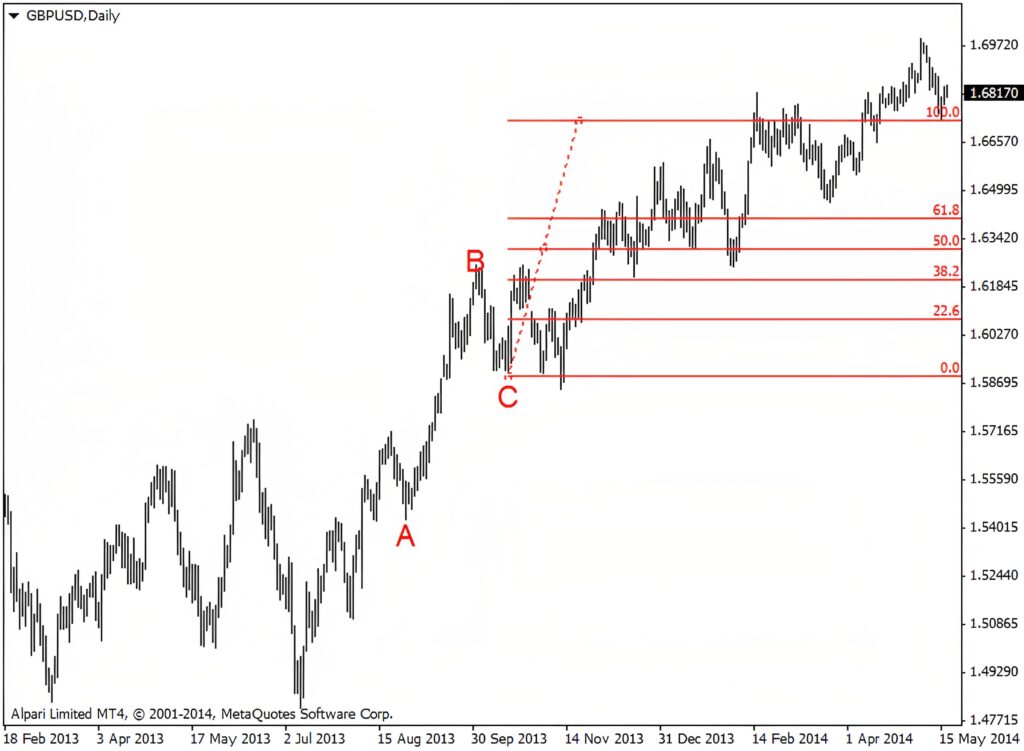
Como usar as retrações de Fibonacci em trading
Você pode usá-las dessa forma:
- Identifique os pontos altos e baixos: encontre os pontos altos e baixos significativos do movimento do preço do ativo.
- Trace os níveis de retração de Fibonacci: use uma ferramenta de gráficos para traçar os níveis de retração de Fibonacci entre os pontos altos e baixos. Os níveis são derivados da sequência de Fibonacci e incluem 23,6%, 38,2%, 50%, 61,8% e 100%.
- Identifique níveis de suporte e resistência: com a retração dos preços, eles podem encontrar suporte ou resistência em um dos níveis de Fibonacci.
- Tome decisões de trading: se os preços ultrapassarem um nível de suporte ou resistência, os traders podem escolher entrar ou sair de uma negociação.
Exemplo usando ouro:
Vamos imaginar que o preço do ouro teve um movimento significativo de $1.500 para $1.800. O ponto mais baixo seria de $1.500 e o ponto mais alto seria de $1.800.
Ao traçar os níveis de retração de Fibonacci, é possível ver que o preço do ouro está encontrando suporte no nível de retração de 50%, que está próximo de $1.650. Nesse caso, o trader pode considerar assumir uma posição de compra em ouro, com uma ordem de stop loss colocada abaixo do nível de Fibonacci de 50%.
Benefícios da Estratégia de Retração de Fibonacci para Traders Experientes
A estratégia de retração de Fibonacci oferece várias vantagens para traders experientes que buscam tomar decisões informadas. Aqui estão alguns dos principais benefícios:
Identificação de Níveis de Suporte e Resistência:
A estratégia de retração de Fibonacci ajuda os traders a identificar possíveis níveis de suporte e resistência, cruciais para determinar movimentos de preço e definir pontos de entrada e saída. Por exemplo, se uma ação está em tendência de alta e recua para um nível Fibonacci importante, isso pode sinalizar uma oportunidade de compra. Essa compreensão mais profunda da estrutura do mercado torna esta estratégia uma ferramenta valiosa no arsenal de um trader.
Melhor Gestão de Risco:
Ao fornecer pontos claros de entrada e saída, a estratégia de retração de Fibonacci melhora a gestão de risco. Os traders podem definir ordens de stop-loss em níveis Fibonacci importantes, limitando assim sua exposição ao risco. Por exemplo, colocar um stop-loss abaixo do nível de retração de 78,6% ajuda a proteger o capital e pode levar a lucros mais consistentes e perdas menores ao longo do tempo.
Melhor Sincronização de Mercado:
Os níveis de retração de Fibonacci podem melhorar significativamente a sincronização de mercado de um trader ao indicar possíveis pontos de reversão. Por exemplo, se uma paridade de moedas atingir um nível de retração de 61,8%, isso pode sinalizar uma reversão de tendência, proporcionando um momento oportuno para entrar ou sair de uma posição. Isso pode aprimorar bastante o processo de tomada de decisão de um trader.
Aumento da Confiança nas Decisões de Negociação:
A estratégia de retração de Fibonacci pode aumentar a confiança dos traders ao oferecer uma base sólida e matemática para análise. Por exemplo, a previsibilidade da sequência de Fibonacci pode ajudar os traders a se sentirem mais seguros em suas previsões, levando a decisões de negociação mais precisas e desempenho geral aprimorado.
Aplicação Prática da Estratégia de Retração de Fibonacci na Negociação
A estratégia de retração de Fibonacci é versátil e aplicável em diversos mercados financeiros. Aqui estão alguns exemplos práticos:
Negociação no Mercado de Ações:
Na negociação de ações, os níveis de Fibonacci ajudam a identificar pontos de entrada e saída. Por exemplo, se uma ação disparar e depois recuar para um nível de retração de 38,2%, um trader pode ver isso como uma oportunidade de compra, antecipando a continuação da tendência de alta.
Negociação Forex:
No mercado Forex, os níveis de retração de Fibonacci podem identificar áreas potenciais de suporte e resistência. Por exemplo, se a paridade EUR/USD cair e depois recuar para o nível de 50%, um trader pode considerar isso como um ponto de entrada potencial para uma posição longa, esperando que o par se recupere.
Negociação de Commodities e Futuros:
Na negociação de Commodities e Futuros, como ouro ou petróleo, os níveis de retração de Fibonacci podem ajudar a determinar pontos estratégicos de entrada e saída. Por exemplo, após um declínio significativo nos preços do ouro, uma retração para o nível de 61,8% pode sugerir uma oportunidade de compra.
Negociação de Criptomoedas:
No mercado de Criptomoedas, os níveis de retração de Fibonacci podem ser usados para identificar potenciais suporte e resistência em ativos voláteis como Bitcoin ou Ethereum. Por exemplo, se o Bitcoin cair e depois recuar para o nível de 50%, os traders podem ver isso como um sinal de compra, antecipando uma recuperação.
Exemplo Hipotético: Estratégia de Negociação com Retração de Fibonacci
Identifique a Tendência: Suponha uma tendência de alta com máximas e mínimas mais altas.
Selecione Pontos de Oscilação: Escolha uma oscilação baixa significativa (1.2000) e uma oscilação alta (1.2500).
Desenhe os Níveis de Fibonacci:
- 0%: 1.2500 (oscilação alta recente)
- 23.6%: ~1.2382
- 38.2%: ~1.2309
- 50%: 1.2250
- 61.8%: ~1.2191
- 78.6%: ~1.2118
- 100%: 1.2000 (oscilação baixa recente)
Plano de Negociação:
- Ponto de Entrada: Entre em uma posição longa em torno do nível de retração de 61,8% (1.2191) se for observado um sinal de reversão de alta.
- Stop Loss: Coloque o stop loss logo abaixo do nível de 78,6% (1.2118).
- Níveis de Take Profit:
- Take Profit 1: Defina no nível de 38,2% (1.2309).
- Take Profit 2: Defina no nível de 0% (1.2500).
Gestão de Risco:
Razão Risco-Retorno: Se a entrada for em 1.219 e o stop-loss em 1.2118 (risco de 73 pips), e o Take Profit 1 for em 1.2309 (retorno de 118 pips), a razão risco-retorno é aproximadamente 1:1.6.
Como Incorporar a Gestão de Risco com Níveis de Retração de Fibonacci
Tamanho da Posição: Determine o tamanho da posição com base no saldo da conta e na tolerância ao risco. Por exemplo, arrisque no máximo 2% do seu capital em uma única negociação.
Ordens de Stop-Loss: Sempre defina ordens de stop-loss ligeiramente abaixo dos níveis de Fibonacci significativos, como o nível de 78,6%, para limitar as perdas potenciais.
Razão Risco-Retorno: Almeje uma razão risco-retorno favorável (por exemplo 1:2). Ajuste os níveis de take profit com base nas extensões de Fibonacci para garantir que os retornos potenciais superem os riscos.
Diversificação: Espalhe o risco diversificando em diferentes ativos ou pares de moedas, evitando a concentração excessiva em uma única negociação.
Evite Reações Emocionais: Siga seu plano de gestão de risco e evite ajustá-lo com base em emoções ou flutuações de mercado de curto prazo. Abstenha-se de negociar com revanchismo após perdas.
Limitações da Estratégia de Negociação Fibonacci
Falta de Base Científica: A sequência de Fibonacci, embora matematicamente interessante, não tem conexão inerente ao comportamento do mercado, tornando seu poder preditivo incerto.
Dependência Excessiva de Padrões Históricos: Os níveis de Fibonacci são baseados em movimentos de preços anteriores, que nem sempre prevêem tendências futuras com precisão.
Subjetividade na Aplicação dos Níveis: Diferentes traders podem aplicar os níveis de Fibonacci de maneira diferente, levando a interpretações e resultados variados.
Sinais Falsos: A estratégia pode gerar sinais falsos, levando a negociações desnecessárias ou oportunidades perdidas, especialmente para traders menos experientes.
Poder Preditivo Limitado: Embora úteis na identificação de suporte e resistência, os níveis de Fibonacci não fornecem insights sobre o sentimento do mercado ou movimentos futuros de preços.
Falha em Considerar a Dinâmica do Mercado: A estratégia não considera fatores externos, como eventos, notícias ou indicadores econômicos, o que pode impactar significativamente a dinâmica do mercado.
Incompatibilidade com Outras Estratégias: As suposições subjacentes à estratégia de Fibonacci podem não se alinhar com outros métodos de negociação, limitando sua eficácia quando combinada com outras estratégias.
Uso Excessivo e Overtrading: Sua simplicidade e apelo visual podem levar ao uso excessivo, resultando em custos de transação mais altos e lucratividade reduzida por conta de overtrading.
Projeções de Fibonacci
São uma ferramenta de análise técnica que usa a sequência de Fibonacci para prever níveis de suporte e resistência no movimento futuro dos preços de um ativo. A sequência de Fibonacci é uma série de números em que cada número é a soma dos dois números anteriores, começando com 0 e 1. Ao traçar esses números em um gráfico, os traders podem identificar os principais níveis em que o preço do ativo pode encontrar resistência ou suporte.
As projeções de Fibonacci proporcionam informações para a tomada de decisões e são usadas por traders em Forex, ações, commodities e outros mercados financeiros. Os níveis-chave identificados podem ajudá-los a encontrar possíveis pontos de entrada e saída, bem como a definir ordens de stop-loss.
Os investidores usam essas projeções como uma ferramenta complementar, juntamente com outros indicadores de análise técnica e fundamental. Lembre-se que as projeções de Fibonacci não são uma garantia do desempenho futuro do mercado, mas um instrumento para ajudar a conhecer o comportamento do mercado passado.
No geral, a projeção de Fibonacci é uma ferramenta valiosa para traders e investidores que desejam conhecer os possíveis movimentos do mercado para determinarem suas ações.
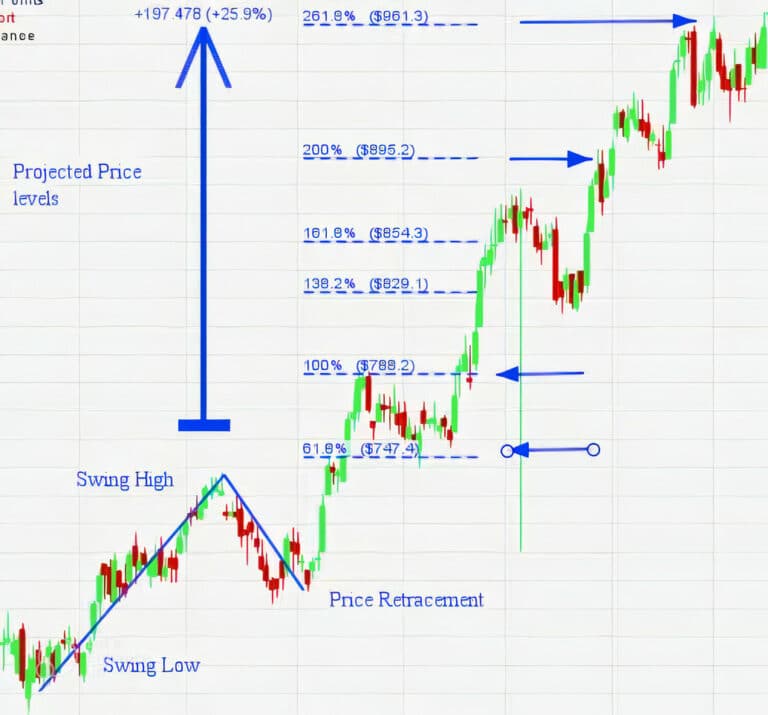
Leque de Fibonacci
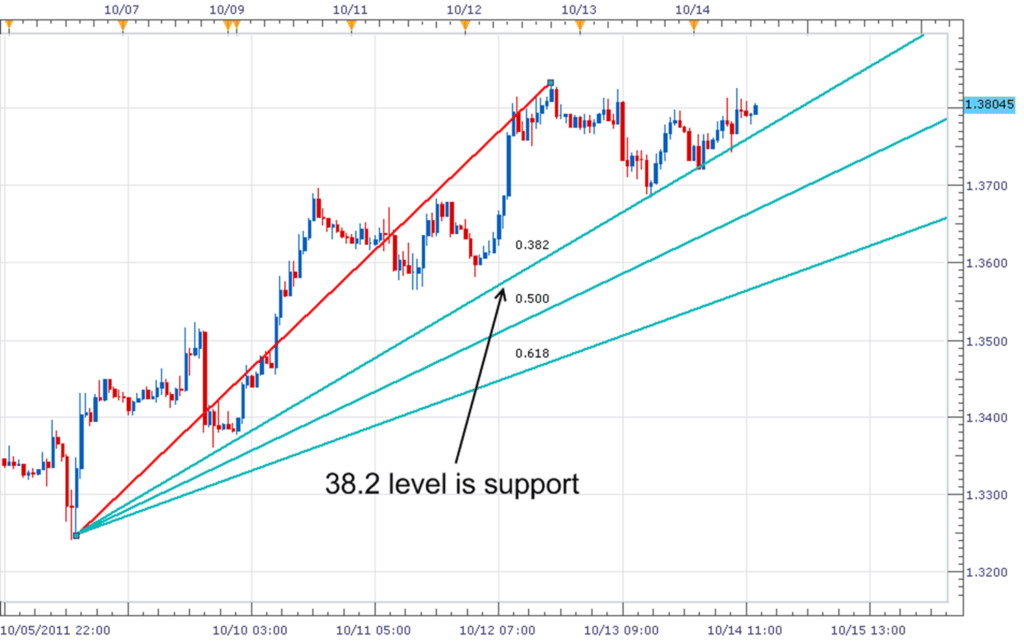
É uma ferramenta de análise técnica que utiliza linhas de retração de Fibonacci para identificar níveis de suporte e resistência na ação de preço de um ativo. Ela é usada desenhando uma linha de tendência entre dois pontos extremos e dividindo a distância vertical com as principais razões de Fibonacci de 23,6%, 38,2%, 50%, 61,8% e 100%.
Estas linhas podem mostrar áreas onde o preço pode encontrar suporte ou resistência. Se a tendência da ação do preço do ativo for para cima, o leque de Fibonacci pode ser usado para identificar níveis potenciais de suporte. Por outro lado, se a ação do preço estiver tendendo para baixo, ele pode ser usado para identificar níveis de resistência.
O leque de Fibonacci é usado para decidir sobre a compra ou venda de um ativo. Esse é um recurso útil para aqueles que seguem uma estratégia de trading baseada em impulso (momentum) ou no acompanhamento de tendências, já que pode mostrar os principais níveis em que a tendência pode reverter ou se manter. A combinação de análise de tendência e níveis de retração de Fibonacci faz com que essa seja uma ferramenta poderosa para a análise técnica.
Resumo
A estratégia de trading de Fibonacci é um método de análise técnica que considera as relações matemáticas entre números sucessivos de Fibonacci para encontrar níveis potenciais de suporte e resistência na ação do preço de um ativo. Ela está baseada na ideia de que os preços tendem a refazer uma parte previsível de um movimento e que depois continuam se movimentando na direção original. A estratégia envolve identificar os principais níveis de Fibonacci, como os níveis de retração de 38,2%, 50% e 61,8%, e usá-los para tomar decisões de trading.
Os traders que usam esta estratégia procuram frequentemente a ação do preço para confirmar a validade dos níveis de Fibonacci, tentando encontrar saltos ou reversões de preços nestes níveis. Se a ação do preço confirmar os níveis, eles podem entrar em posições ou ajustar as existentes.
Em linhas gerais, a estratégia de trading de Fibonacci pode ser uma ferramenta útil para melhorar a análise e ajudar nas escolhas de trading. No entanto, como em qualquer abordagem de análise técnica, esse indicador deve ser combinado com outros métodos de análise e não usado isoladamente.
Pontos principais:
- A sequência de Fibonacci e a Proporção Áurea são conceitos matemáticos que podem ser aplicados aos mercados financeiros para análise técnica.
- Os traders utilizam os níveis de retração de Fibonacci para identificar potenciais níveis de suporte e resistência onde o preço de um ativo pode encontrar um piso ou teto após um movimento significativo para cima ou para baixo.
- As extensões de Fibonacci podem ser usadas para projetar alvos potenciais de lucro aplicando as proporções de Fibonacci ao movimento de preço anterior.
- As projeções de Fibonacci ajudam a prever futuros níveis de suporte e resistência projetando as proporções de Fibonacci a partir de um movimento de preço significativo.
- O leque de Fibonacci usa linhas de tendência e proporções de Fibonacci para identificar potenciais níveis de suporte e resistência em um mercado em tendência.
- Os traders podem usar os níveis de Fibonacci para tomar decisões informadas sobre entrar ou sair de operações, definir ordens de stop-loss e realizar lucros.
- As estratégias de negociação de Fibonacci devem ser usadas em conjunto com outras ferramentas de análise técnica e análise fundamental e não devem ser exclusivamente confiadas para tomar decisões de negociação.
- A sequência de Fibonacci e suas proporções são encontradas em muitos fenômenos naturais, e sua aplicação nos mercados financeiros baseia-se na ideia de que os preços tendem a retraçar uma porção previsível de um movimento antes de continuar na direção original.




